Statistik ist ein unverzichtbares Werkzeug für Data Science. Statistische Methoden sind notwendig, um Daten zu sammeln, zu analysieren und Schlussfolgerungen aus ihnen zu ziehen. Ohne Statistik wäre es unmöglich, die komplexen Datensätze zu verstehen, die bei der Data Science eingesetzt werden. In diesem Artikel führe ich in die Grundlagen der Wahrscheinlichkeit ein.
Statistik ist allgemein die Wissenschaft der Datenanalyse. Sie umfasst die Sammlung, Organisation, Analyse, Interpretation und Präsentation von Daten. Statistik kann verwendet werden, um ein breites Spektrum von Problemen zu lösen, von der Planung einer Marketingkampagne bis hin zur Erforschung der Auswirkungen von neuen Medikamenten.
Statistiken werden verwendet, um die Häufigkeit oder Intensität von etwas zu ermitteln. Sie können auch verwendet werden, um einen möglichen Zusammenhang zwischen zwei Dingen zu untersuchen.
In der Statistik wird häufig mit Stichproben gearbeitet. Ist ein Datensatz zu groß, um ihn als Ganzes zu untersuchen, dann zieht man aus diesem Datensatz eine Stichprobe. Diese Stichprobe wird untersucht und dann können daraus Schlussfolgerungen für den gesamten Datensatz, die sogenannte Grundgesamtheit, gezogen werden.
Deskriptive Statistik
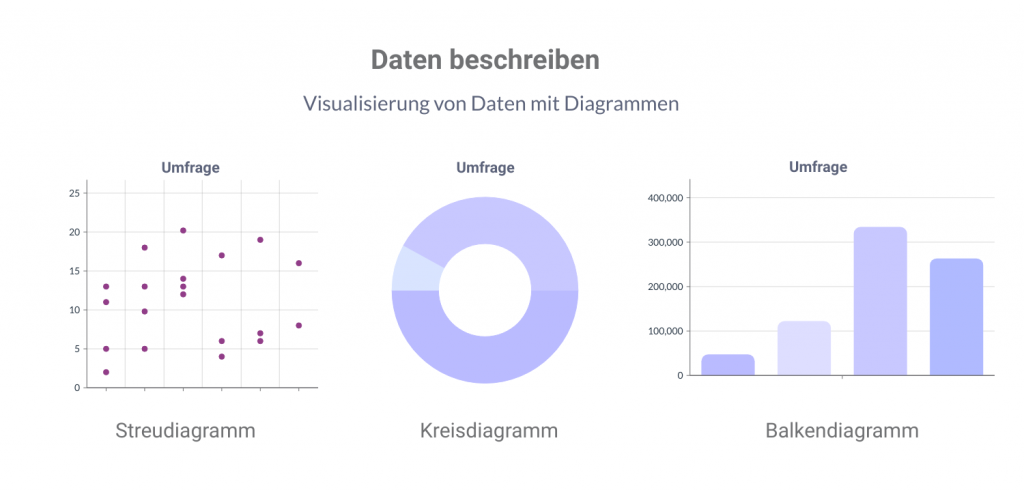
Definitionsgemäß bedeutet deskriptiv so viel wie beschreibend. Deskriptive Statistiken befassen sich mit der Erhebung, Organisation und Visualisierung von Daten. Dazu gehören Tabellen, Grafiken und die Bestimmung relevanter Kennzahlen, die als Maßzahlen oder Parameter bezeichnet werden. Mithilfe dieser Kennzahlen kann man die zentrale Tendenz, Streuung und Verteilung einer Stichprobe beschreiben. Sie können verwendet werden, um Trends und Muster im Datensatz zu finden.
Die deskriptive Statistik befasst sich mit der Beschreibung eines Datensatzes und seiner Attribute. Ziel der deskriptiven Statistik ist, die empirischen Daten zu veranschaulichen, daher wird sie umgangssprachlich auch als beschreibende Statistik bezeichnet.
Es gibt drei Arten von Kenngrößen, die in der deskriptiven Statistik Anwendung finden:
- Lagemaße
Ermittlung der zentralen Tendenz der Daten
Bsp.: Mittelwert, Median und Modus - Streuungsmaße
Zur Ermittlung der Streuung
Bsp.: Varianz, Standardabweichung - Zusammenhangsmaße
Stärke und gegebenenfalls Richtung des Zusammenhangs zweier Variablen
Bsp.: Korrelationskoeffizienten
Induktive Statistik
Die Hauptfunktion der induktiven Statistik besteht darin, Schlüsse von einer Zufallsstichprobe auf die zugrunde liegende Grundgesamtheit zu übertragen, welche durch Testverfahren wie Hypothesentests und weitere Methoden untermauert werden können.
In der induktiven Statistik wird die Zuverlässigkeit von Ergebnissen, die aufgrund von Stichproben ermittelt werden, durch eine Wahrscheinlichkeitsrechnung beurteilt. Mit dieser Methode kann sichergestellt werden, dass Ergebnisse, die aufgrund von Stichproben gewonnen werden, auf die Grundgesamtheit übertragbar und auch inhaltlich korrekt sind.
Im Gegensatz zur deskriptiven Statistik liefert die induktive Statistik aus einer kleinen Auswahl von Daten (Stichprobe) Informationen über die größeren Daten (Grundgesamtheit), aus denen die Stichprobe stammt.
Unterschied zwischen deskriptiver und induktiver Statistik
Die Unterscheidung zwischen deskriptiver und induktiver Statistik kann zunächst Verwirrung erzeugen, obwohl die Unterscheidung eigentlich leicht verständlich ist. Die deskriptive Statistik macht es möglich, die Stichproben-Daten übersichtlich darzustellen, um die weitere Untersuchung vorzubereiten. Im Gegensatz dazu bietet die induktive Statistik ein tieferes Verständnis, indem sie wahrscheinlichkeitstheoretische Methoden einsetzt, um die allgemeine Gültigkeit einer Erkenntnis zu bestätigen. Die deskriptive Statistik beschreibt die Charakteristika von Datensätzen. Die induktive Statistik wird verwendet, um daraus Schlüsse auf die zugrunde liegende Grundgesamtheit ziehen zu können.
Beispiel:
Wir haben einen sozialökonomischen Datensatz, der Männer im Alter von 20-40 Jahren beschreibt, die in einer typischen Kleinstadt in Hessen wohnen. Mit den Methoden der deskriptiven Statistik können wir nun die Charakteristika der Grundgesamtheit dieser Männer beschreiben, wie zum Beispiel das durchschnittliche Einkommen oder den Bildungsstand. Mit den wahrscheinlichkeitstheoretischen Methoden der induktiven Statistik können wir dagegen Schlussfolgerungen über die Grundgesamtheit der Männer ziehen, die zwischen 20 und 40 Jahre alt sind und in allen Kleinstädten in Hessen wohnen. Wir testen mit der induktiven Statistik also die allgemeine Gültigkeit der Stichprobe.

Schreibe einen Kommentar