Herzlich willkommen in der beeindruckenden Welt der Datenanalyse, in der Algorithmen wie k-Means die unüberschaubare Vielfalt riesiger Datenmengen in übersichtlich strukturierte und leichter verständliche Informationen umwandeln. Ganz gleich, ob Sie ein Unternehmer auf der Suche nach neuen Marktsegmenten sind oder ein Fotograf, der seine Aufnahmen optimieren möchte – der k-Means Algorithmus hilft bei der Gruppierung ähnlicher Daten. In diesem Blog-Artikel werde ich den k-Means Algorithmus entschlüsseln und Ihnen aufzeigen, wie er dazu beiträgt, verborgene Strukturen und Zusammenhänge in Ihren Daten zu entdecken.
Der k-Means Algorithmus ist ein weitverbreitetes maschinelles Lernverfahren zur Clusteranalyse, das Datensätze in sinnvolle Gruppen (Cluster) unterteilt. Durch die Anwendung von k-Means können Sie wertvolle Erkenntnisse gewinnen und fundierte Entscheidungen treffen, basierend auf der Struktur und den Beziehungen innerhalb Ihrer Daten. In diesem leicht verständlichen Leitfaden werden wir den k-Means Algorithmus Schritt für Schritt erklären und zeigen, wie Sie ihn für Ihre eigenen Projekte einsetzen können. Bleiben Sie dran, um mehr über diese leistungsstarke Methode der Datenanalyse zu erfahren und Ihre Fähigkeiten im Umgang mit großen Datensätzen auf die nächste Stufe zu heben!
Was ist der k-Means Algorithmus?
Der k-Means Algorithmus ist ein iteratives Verfahren zur Clusterbildung, das darauf abzielt, Datenpunkte in k separate Gruppen (Cluster) zu unterteilen. Diese Gruppen basieren auf der Ähnlichkeit der Datenpunkte, wobei die Distanz (z.B. euklidische Distanz) zwischen ihnen als Maß für die Ähnlichkeit verwendet wird.
In dem Ausdruck k-Means, gibt k die Anzahl der Cluster in den Daten an. Da der k-Means Algorithmus diese nicht vorgibt, muss diese Größe zunächst bestimmt werden. Die Eigenschaften der Cluster hängt stark von der Genauigkeit des festgelegten k-Werts ab. Sofern die Daten in zwei oder drei Dimensionen vorliegen, lässt sich ein angemessener Bereich von k-Werten visuell bestimmen. Bei Datensätzen, die über mehr als drei Dimensionen verfügen, können wir auf mathematische Verfahren zurückgreifen, um einen geeigneten K-Wert zu ermitteln. Eine solche Methode stellt etwa der Silhouettenkoeffizient dar.
Anwendungen des k-Means Algorithmus
Der k-Means Algorithmus findet Anwendung in einer Vielzahl von Bereichen, wie beispielsweise:
- Marktforschung: Segmentierung von Kunden oder Produkten aufgrund ihrer Eigenschaften.
- Bildverarbeitung: Komprimierung und Segmentierung von Farben in Bildern.
- Textanalyse: Gruppierung von ähnlichen Dokumenten oder Artikeln.
- Anomalieerkennung: Identifizierung von ungewöhnlichen Verhaltensmustern oder Ausreißern in Datensätzen.
Schritt-für-Schritt-Anleitung zum k-Means Algorithmus
Der k-Means-Algorithmus funktioniert, indem er Clusterzentren in einem n-dimensionalen Diagramm positioniert und anschließend kontrolliert, ob eine Verschiebung in irgendeine Richtung zu einem neuen Zentrum mit erhöhter Dichte führt, das heißt, mit einer größeren Anzahl von Datenpunkten in seiner Umgebung.
Die Clusterzentren wandern von Gebieten mit niedriger Dichte hin zu Gebieten mit höherer Dichte, bis alle Zentren in einem Bereich mit der höchsten lokalen Dichte liegen. Diese Bereiche stellen das jeweils korrekte Zentrum eines Clusters dar. Jeder Cluster weist dann die maximale Anzahl an Punkten in unmittelbarer Nähe seines Zentrums auf.
Schritt 1 – Initialisierung:
Wir erstellen einen zufälligen, zweidimensionalen Datensatz und geben die Datenpunkte in einem Diagramm aus.

Schritt 2 – Bestimmung k-Cluster:
Wir legen die Anzahl der Cluster mit k=3 fest. In unserem Beispiel sind die Cluster durch grüne, rote und blaue Datenpunkte gekennzeichnet. Für diese Anzahl der Cluster (k), in die die Daten unterteilt werden sollen, wählen wir dann zufällig 3 Datenpunkte aus dem Datensatz als initiale Clusterzentren (Centroids) aus.

Schritt 3 – Zuordnung der Datenpunkte:
Wir berechnen die Distanz jedes Datenpunkts zu allen k Centroids und weisen jeden Datenpunkt dem nächstgelegenen Centroid zu, wodurch temporäre Cluster entstehen.
Schritt 4 – Aktualisierung der Centroids:
Wir berechnen den Schwerpunkt (Mittelwert) aller Datenpunkte in jedem temporären Cluster und setzen Sie die neuen Centroids auf diese Schwerpunkte.

Schritt 5 – Wiederholung:
Nun wiederholen wir die Schritte 2 und 3, bis sich die Centroids nicht mehr signifikant verschieben oder eine maximale Anzahl von Iterationen erreicht ist.


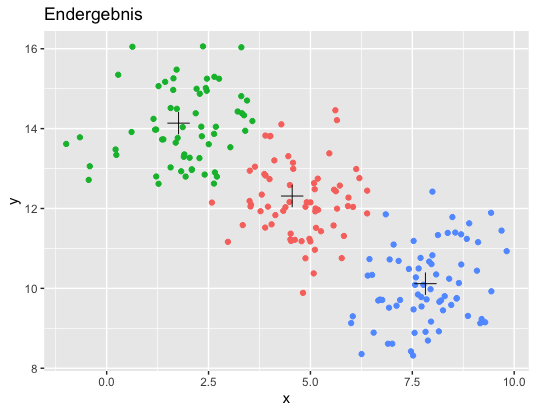
Ergebnis:
Die endgültigen Cluster sind die Gruppen von Datenpunkten, die den stabilen Centroids am nächsten liegen.
Beispiel für den k-Means Algorithmus in R
Hier ist ein R-Code-Beispiel, um die verschiedenen Schritte des k-Means Algorithmus zu visualisieren. Dieser R-Code erstellt einen Beispieldatensatz und führt den k-Means Algorithmus darauf aus. Anschließend wird für jeden Schritt des Algorithmus ein entsprechender Plot erstellt. Sie können diese Plots verwenden, um die verschiedenen Phasen des k-Means Algorithmus zu visualisieren.
# Laden der benötigten Pakete
library(ggplot2)
library(ggrepel)
# Erstellen eines Beispieldatensatzes
set.seed(42)
n <- 67
data <- data.frame(x = c(rnorm(n, mean = 2), rnorm(n, mean = 5), rnorm(n, mean = 8)),
y = c(rnorm(n, mean = 14), rnorm(n, mean = 12), rnorm(n, mean = 10)))
# k-Means Algorithmus
k <- 3
set.seed(42)
centroids <- data[sample(1:nrow(data), k), ]
data$cluster <- apply(data, 1, function(row) {
which.min(sqrt((centroids$x - row["x"])^2 + (centroids$y - row["y"])^2))
})
# Plot 1: Datenpunkte ohne Gruppierung
p1 <- ggplot(data, aes(x = x, y = y)) +
geom_point(color = "blue") +
labs(title = "Datenpunkte ohne Gruppierung")
print(p1)
# Plot 2: Initialisierung der Centroids
p2 <- ggplot(data, aes(x = x, y = y)) +
geom_point(aes(color = factor(cluster))) +
geom_point(data = centroids, aes(x = x, y = y), color = "black", shape = 3, size = 5, show.legend = FALSE) +
labs(title = "Initialisierung der Centroids") +
guides(color = FALSE)
print(p2)
# Plot 3-5: k-Means Algorithmus Iterationen
for (iteration in 1:3) {
# Aktualisiere die Centroids
centroids <- aggregate(data[, c("x", "y")], list(cluster = data$cluster), mean)
# Ordne Datenpunkte den Centroids neu zu
data$cluster <- apply(data, 1, function(row) {
which.min(sqrt((centroids$x - row["x"])^2 + (centroids$y - row["y"])^2))
})
# Plotte die Iteration
p <- ggplot(data, aes(x = x, y = y)) +
geom_point(aes(color = factor(cluster))) +
geom_point(data = centroids, aes(x = x, y = y), color = "black", shape = 3, size = 5, show.legend = FALSE) +
ggrepel::geom_label_repel(data = centroids, aes(x = x, y = y, label = 1:nrow(centroids)), size = 5, show.legend = FALSE) +
labs(title = paste("Iteration", iteration, ": Zuordnung & Aktualisierung")) +
guides(color = FALSE)
print(p)
}
# Plot 6: Endergebnis
p7 <- ggplot(data, aes(x = x, y = y)) +
geom_point(aes(color = factor(cluster))) +
geom_point(data = centroids, aes(x = x, y = y), color = "black", shape = 3, size = 5, show.legend = FALSE) +
labs(title = "Endergebnis") +
guides(color = FALSE)
print(p7)
Mit dem oben bereitgestellten R-Code erhalten Sie sieben Plots:
- Plot 1: Die Datenpunkte ohne Gruppierung
- Plot 2: Die Initialisierung der Centroids
- Plots 3-5: Drei Iterationen des k-Means Algorithmus (Zuordnung und Aktualisierung)
- Plot 6: Das Endergebnis mit den endgültigen Clustern und Centroids
Sie können die Anzahl der Iterationen ändern, indem Sie den Wert in der for-Schleife anpassen. Außerdem können Sie die Größe des Beispieldatensatzes und die Anzahl der Cluster (k) ändern, um unterschiedliche Datensätze und Clustering-Szenarien zu untersuchen.
Fazit
Der k-Means Algorithmus ist ein äußerst nützliches und flexibles Werkzeug, das in zahlreichen Anwendungsbereichen und Branchen genutzt wird, um wertvolle Erkenntnisse aus Datenbeständen zu gewinnen. In diesem Blog-Beitrag haben wir uns mit den Grundlagen des k-Means Algorithmus beschäftigt und seine Funktionsweise anhand eines einfachen, schrittweisen Beispiels erläutert. Wir haben ebenfalls gezeigt, wie Sie den Algorithmus in R implementieren und darstellen können, um die verschiedenen Phasen und Iterationen anschaulicher zu machen.
Dank seiner Einfachheit und Effizienz bleibt der k-Means Algorithmus eine beliebte Methode zur Clusteranalyse und ein wertvolles Werkzeug für Datenwissenschaftler, Analysten und Entscheidungsträger. Durch das Verständnis und die Anwendung des k-Means Algorithmus können Sie verborgene Muster und Zusammenhänge in Ihren Daten aufdecken und fundierte Entscheidungen treffen, die auf der Struktur Ihrer Daten basieren.
Ich hoffe, dass dieser Blog-Artikel Ihnen einen tiefen Einblick in die Anwendung und Funktionsweise des k-Means Algorithmus gegeben hat und dass Sie die erlernten Konzepte erfolgreich in Ihren eigenen Projekten und Analysen anwenden können. Bleiben Sie dran für weitere spannende Artikel und Anleitungen zum Thema maschinelles Lernen und Datenanalyse!

Schreibe einen Kommentar