Clustering-Verfahren

Clustering ist ein Prozess, bei dem ähnliche Elemente oder Objekte aus einem Datensatz in Untergruppen zusammengefasst werden. Dies geschieht häufig, um Daten zu analysieren oder zu visualisieren. Clustering kann auch verwendet werden, um ähnliche Dinge zu finden oder abzugrenzen. Unternehmen können so etwa Kundendaten clustern, um bessere Geschäftsentscheidungen zu treffen.

Cluster-Verfahren sind eine Form des maschinellen Lernens. Wir betrachten hier Cluster-Verfahren als unüberwachtes Lernen (unsupervised learning), bei dem die Einteilung in Klassen nur aufgrund der vorhandenen Daten und ohne speziellen Lernschritt erfolgt. Demnach sind die Daten in dem Datensatz nicht benannt, weshalb Algorithmen prädikative Methoden einsetzen müssen, um Muster, Beziehungen und Verbindungen in dem unverarbeiteten Datensatz zu identifizieren. 

Clustering Algorithmen dienen dazu, Datensätze in Gruppen von Datenpunkten zu unterteilen, welche vorgegebenen Merkmalen entsprechen. Wenn man eine Reihe von Datenpunkten mit spezifischen Merkmalen hat und sie aufgrund dieser Merkmale gruppieren möchte, dann verwendet man Clustering Algorithmen

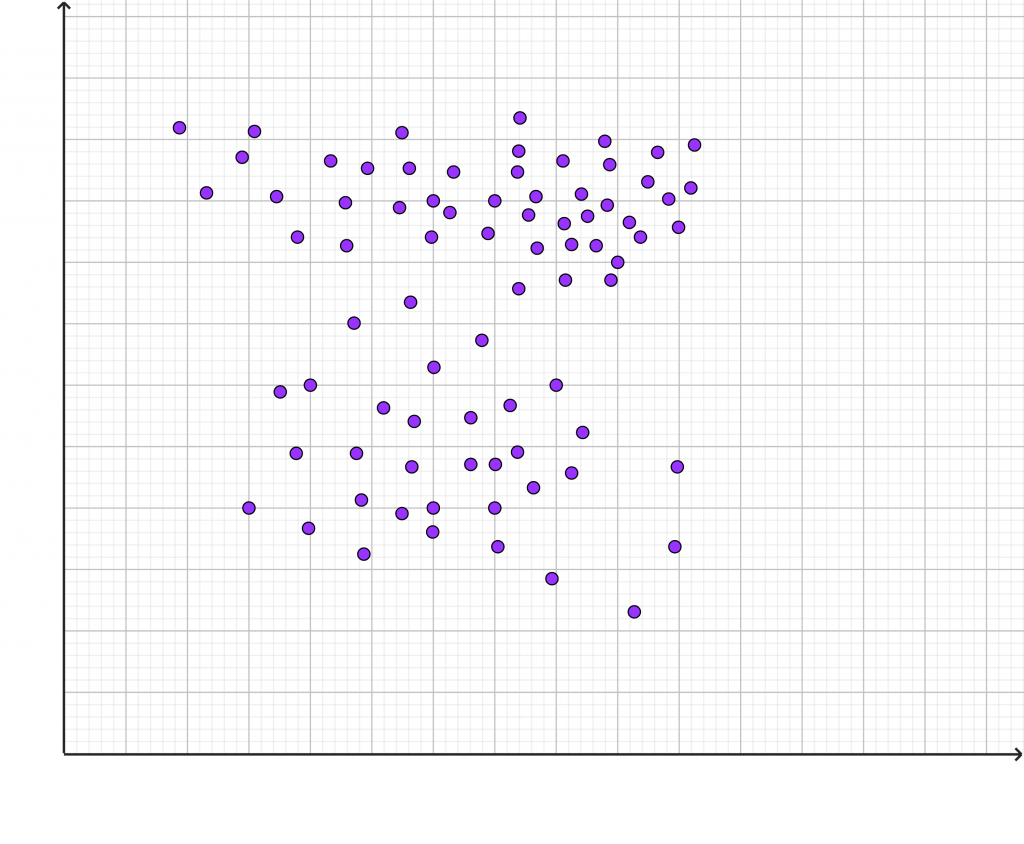
Hierbei wird ein Algorithmus so lange auf einen Datensatz angewendet, bis bestimmte, vorgegebene Bedingungen erfüllt sind. Vorgegebene Bedingungen sind etwa die Anzahl der Cluster oder die Form der Cluster (Ellipsen, freie Form). Ob die Datenpunkte jeweils nur zu einem Cluster gehören oder ob es Überlappungen geben kann (hard oder soft clustering), ist eine weitere mögliche Bedingung.

Man startet mit den gegebenen Daten und trennt sie anhand von Clustering-Algorithmen in verschiedene Gruppen, welche als Cluster bezeichnet werden. Diese Cluster bestehen aus Daten, die weitgehend ähnlich sind. Bei der Betrachtung der Grafik werden mindestens zwei, wahrscheinlich aber auch drei Cluster sichtbar.

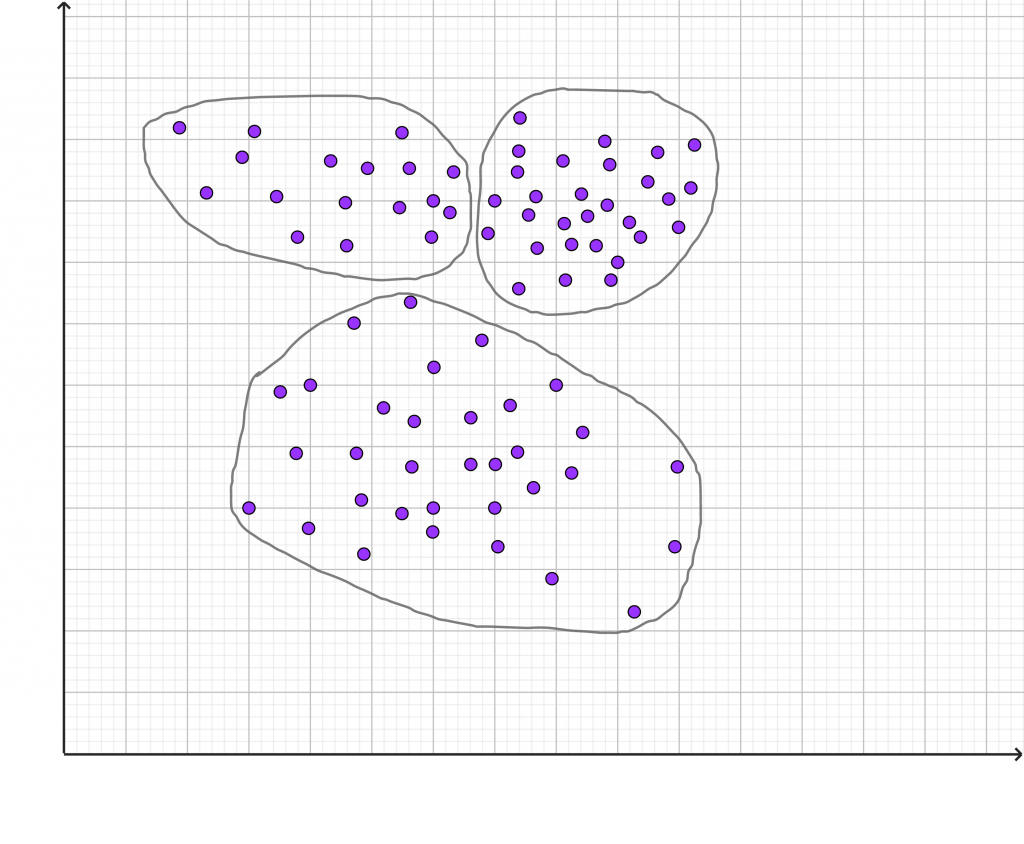
Cluster-Algorithmen arbeiten, indem sie zunächst einen oder mehrere Punkte als „Seed“-Punkte auswählen. Anschließend wird jeder andere Punkt im Datensatz mit den Seed-Punkten verglichen und denjenigen Seed-Punkten zugeordnet, mit denen er am stärksten übereinstimmt. Dieser Prozess wiederholt sich, bis alle Punkte im Datensatz zugeordnet sind. Ein Cluster-Algorithmus kann auf verschiedene Weisen implementiert werden und es gibt viele verschiedene Varianten. Die genaue Implementierung hängt von den Zielen ab, die damit erreicht werden sollen.

Abstandsmaß zwischen Mengen

Ein wichtiger Bestandteil bei der Auswahl der passenden Methode für das Clusterverfahren ist die Abstandsmessung. Wenn wir Punkte in bestimmte Cluster einteilen, benötigen wir ein Abstandsmaß zwischen Mengen. Die Abstandsmessung bestimmt, wie weit entfernt die Objekte in einem Cluster voneinander liegen oder wie weit zwei Cluster voneinander entfernt sind. Sie ist ein wichtiges Kriterium für die Qualität des Clusters. 

Für das Abstandsmaß zwischen Mengen, also den Abstand zwischen zwei Clustern, können unterschiedliche Berechnungsarten herangezogen werden. Je nachdem, welche Punkte man innerhalb der Cluster wählt, können wir folgende Abstände ermitteln:

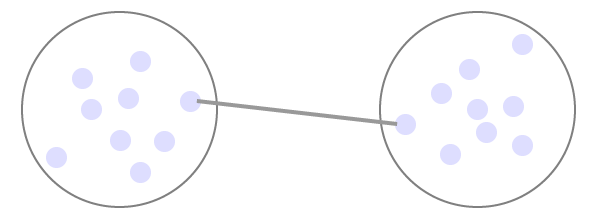
Single Linkage / MIN Metrik:
Abstand der beiden nächstliegenden Punkte

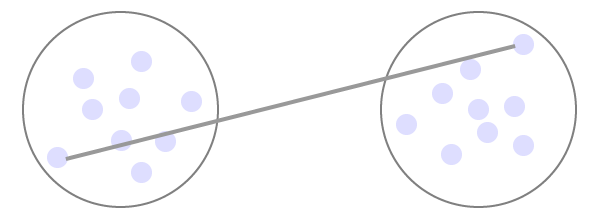
Complete Linkage / MAX Metrik:
Abstand der beiden am weitesten entfernt liegenden Punkte

Centroid Linkage:
Abstand der Schwerpunkte der beiden Cluster

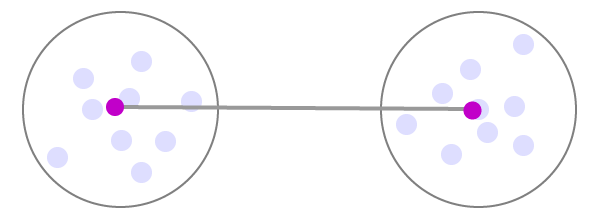
Es gibt verschiedene Arten von Abstandsmessungen, die alle ihre Vor- und Nachteile haben. Die am häufigsten verwendete Methode ist die Euklidische Distanz. Daneben gibt es auch andere, wie zum Beispiel die Manhattan-Distanz oder die Chebyshev-Distanz.

Euklidischer Abstand

Der euklidische Abstand ist eine mathematische Methode zur Berechnung der Entfernung zwischen zwei Punkten in einem dreidimensionalen Raum. Dabei wird die Strecke zwischen den beiden Punkten M (m₁,m₂,…,m_n) und K (k₁,k₂,…,k_n)in einer geraden Linie berechnet. Dabei ist n die Dimension des jeweiligen Raumes. Der euklidische Abstand ist die kürzeste Entfernung zwischen diesen beiden Punkten.

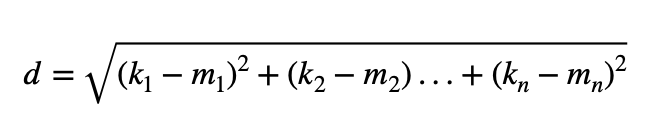
Das Abstandsmaß wird für jedes zu vergleichende Merkmal und alle Daten berechnet. Auf diese Weise kann für jedes Merkmal bestimmt werden, welche Daten sich innerhalb einer Datenmenge am meisten ähneln und welche am unterschiedlichsten sind.  

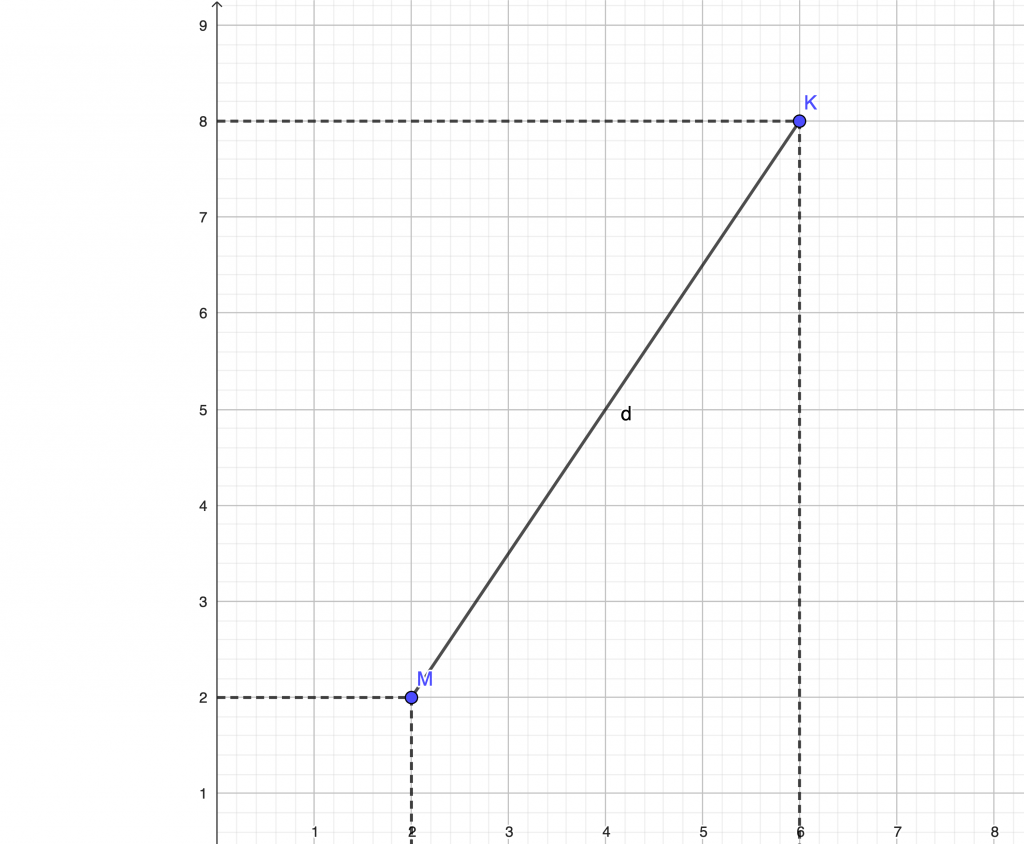
Im zweidimensionalen Raum berechnet sich der euklidische Abstand zwischen den Punkten M(2,2) und K(6,8) wie folgt:

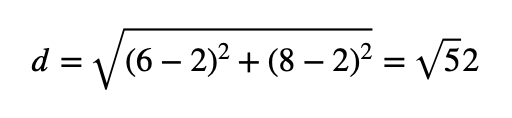
Es gibt zahlreiche Algorithmen, um Daten in Cluster einzuteilen. Welche Methode sich am besten eignet, hängt generell von der Fragestellung ab. Oftmals werden die Ergebnisse verschiedener Verfahren am Ende miteinander verglichen, um das beste Verfahren richtig zu ermitteln. Die bekanntesten Vertreter sind: 

• Hierarchisches Clustering (Dendogramme)
• k-Means Algorithmus
• k-Nearest-Neighbour Algorithmus